Nine unit circles are packed into a square, tangent to their neighbors and to the square. What is the length of the longest smooth path connecting two opposite corners of the square?
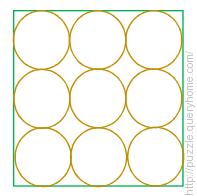
Assumptions:
- The path must be continuous and follow the lines in the diagram; that is, it must be made up of portions of either the circles or the outside square.
- The path may not change direction suddenly.
- The path may not contain any loops.
- The path may not touch or cross itself at any point.
