11 was the original number
lets look at the numbers first, see this table:
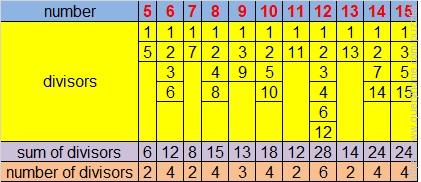
Neel: "I don't know the original number." - number of divisors are either 2 or 4, odd numbers (3 & 6) now excluded as Neel doesn't know the number, numbers 2&4 repeated in last raw of the table and he can't see which one is correct,
Nitin: "I don't know the original number either." - sum of divisors are either 12 or 24, odd numbers (6,8,14,15,18) excluded as Nitin doesn't know the number, numbers 12&24 repeated in the 3rd raw of the table and he can't see which one is correct,
We have now 4 numbers left- 6 (12/4), 11 (12/2), 14 (24/4) and 15 (24/4)
Neel: "Now I know the original number." - odd number is left among 4 numbers, which is number 2, the original number is 11
Nitin: "Me too!"- same logic, understands that it is number 11
