top button
Flag Notify
    Connect to us
      Site Registration

Site Registration

ABCD is a quadrilateral. Point O is along AD. A semicircle has a diameter along AD.............what is the length of AD?

0 votes
361 views

ABCD is a quadrilateral. Point O is along AD. A semicircle has a diameter along AD and is tangent to the sides AB, BC, and CD. If AB = 9, CD = 16, and AO = OD, what is the length of AD?

enter image description here

posted Jan 6, 2021 by Aman

Looking for solution? Promote on:
Facebook Share Button Twitter Share Button LinkedIn Share Button




Similar Puzzles
0 votes
If each semicircle has a diameter equal to 2, what is the length of AD?

Semicircle AB is flipped upside down and translated horizontally so the new semicircle CD is tangent to AB, as shown. The line through AB is tangent to the semicircle CD and the line through CD is tangent to the semicircle AB.
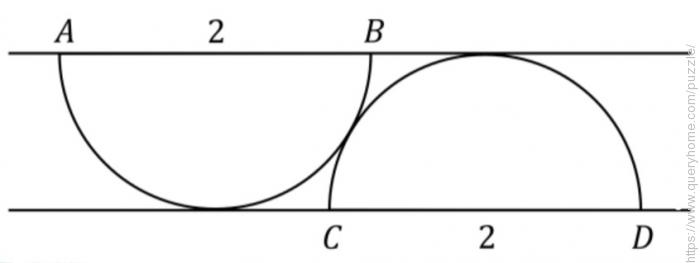
enter image description here

If each semicircle has a diameter equal to 2, what is the length of AD?
Express your answer in the form √x + √y for positive integers x < y.

+1 vote
Quadrilateral ABCD has AD = BC, ∠A + ∠B = 90°, AB = 20, CD = 10, as shown below.What is the area of ABCD?

Quadrilateral ABCD has AD = BC, ∠A + ∠B = 90°, AB = 20, CD = 10, as shown below.

enter image description here

What is the area of ABCD?

+1 vote
A semicircle with radius a is inscribed in a rectangle with its diameter along one...........Solve for the value of a/b.

A semicircle with radius a is inscribed in a rectangle with its diameter along one side of the rectangle. A circle with radius b is then inscribed so it is tangent to the rectangle and the semicircle, as shown.
Solve for the value of a/b.

enter image description here

0 votes
Rectangle ABCD is made up of 5 equal rectangles, as shown. Point E is on side CD, and AD = 10. What is the area.........

Rectangle ABCD is made up of 5 equal rectangles, as shown. Point E is on side CD, and AD = 10.
What is the area of triangle ABE?
enter image description here

0 votes
In rectangle ABCD, point G is the midpoint of AD, and points E and F trisect...........what is the area of triangle HIG?

In rectangle ABCD, point G is the midpoint of AD, and points E and F trisect BC. The diagonal BD intersects GE at H and GF at I. If the area of ABCD is 10, what is the area of triangle HIG?

enter image description here

...