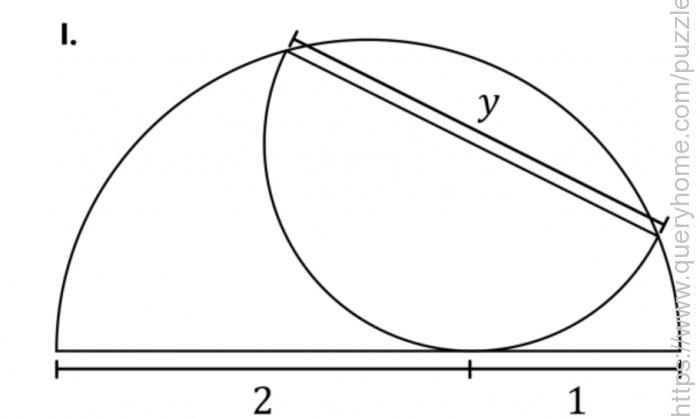
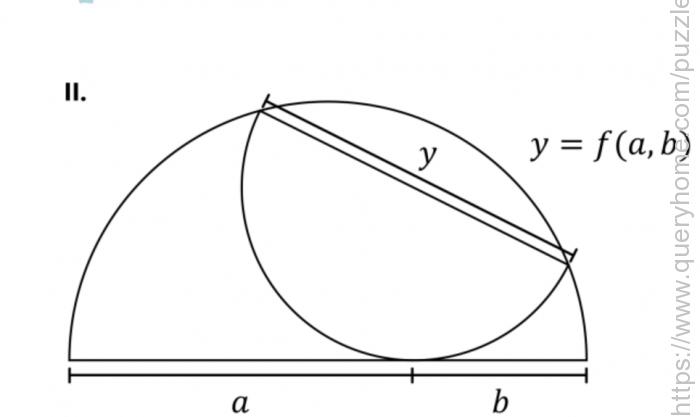
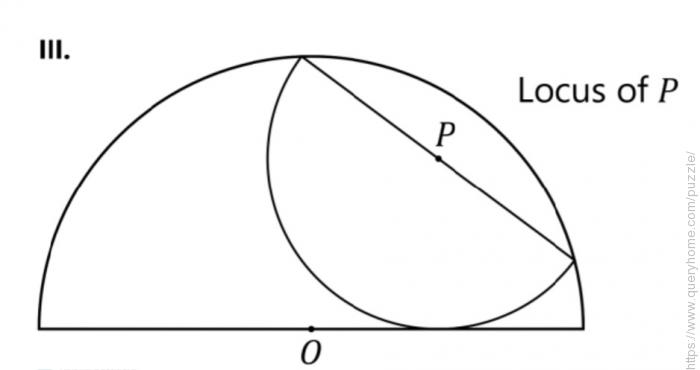
A semicircle contains an inscribed semicircle, as shown, dividing its diameter into lengths of 2 and 1. The question has three parts.
I. What is the value y equal to the length of the inscribed semicircle’s diameter?
II. Solve again for the general case if the large diameter is divided into lengths of a and b.
III. Let P be the center of the inscribed semicircle. Solve for the locus of P–that is the set of points P for all possible inscribed semicircles.