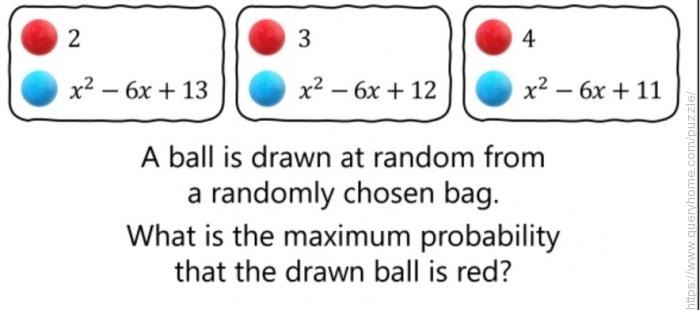
Each of three bags b1, b2, b3 contains only red and blue balls in the quantities:
Bag b1
red = 2 balls
blue = x2 – 6x + 13 balls
Bag b2
red = 3 balls
blue = x2 – 6x + 12 balls
Bag b3
red = 4 balls
blue = x2 – 6x + 11 balls
A ball is drawn at random from a randomly chosen bag. What is the maximum probability the drawn ball is red?