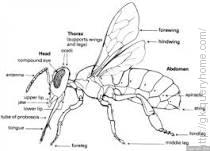
Five eyes
Four wings: The front and rear wings hook together to form one big pair of wings and unhook for easy folding when not flying. Five eyes: Yes, honey bees have five eyes, two large compound eyes and three smaller ocelli eyes in the centre of their head.