Searching an Element in a Rotated Sorted Array Explain with example?

Question

Find the count k by which array has been rotated in the rotated sorted array. So for example we have sorted array as 2,3,6,12, 15, 18. Now suppose the array is rotated k times ( we don’t know k), such that array becomes 15, 18,2,3,6,12 We have to find K?

Answer 1

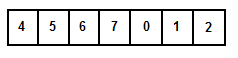
Suppose a sorted array is rotated at some pivot unknown to you beforehand. (i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2). How do you find an element in the rotated array efficiently?

At first look, we know that we can do a linear search in O(n) time. But linear search does not need the elements to be sorted in any way.

First, we know that it is a sorted array that’s been rotated. Although we do not know where the rotation pivot is, there is a property we can take advantage of. Here, we make an observation that a rotated array can be classified as two sub-array that is sorted (i.e., 4 5 6 7 0 1 2 consists of two sub-arrays 4 5 6 7 and 0 1 2.

Do not jump to conclusion that we need to first find the location of the pivot and then do binary search on both sub-arrays. Although this can be done in O(lg n) time, this is not necessary and is more complicated.

In fact, we don’t need to know where the pivot is. Look at the middle element (7). Compare it with the left most (4) and right most element (2). The left most element (4) is less than (7). This gives us valuable information — All elements in the bottom half must be in strictly increasing order. Therefore, if the key we are looking for is between 4 and 7, we eliminate the upper half; if not, we eliminate the bottom half.

When left index is greater than right index, we have to stop searching as the key we are finding is not in the array.

Since we reduce the search space by half each time, the complexity must be in the order of O(lg n). It is similar to binary search but is somehow modified for this problem. In fact, this is more general than binary search, as it works for both rotated and non-rotated arrays.

int rotated_binary_search(int A[], int N, int key) {
  int L = 0;
  int R = N - 1;

  while (L <= R) {
    // Avoid overflow, same as M=(L+R)/2
    int M = L + ((R - L) / 2);
    if (A[M] == key) return M;

    // the bottom half is sorted
    if (A[L] <= A[M]) {
      if (A[L] <= key && key < A[M])
        R = M - 1;
      else
        L = M + 1;
    }
    // the upper half is sorted
    else {
      if (A[M] < key && key <= A[R])
        L = M + 1;
      else
        R = M - 1;
    }
  }
  return -1;
}