Quicksort is a sorting algorithm that uses the divide and conquer strategy. This algorithm finds the element called pivot , that partitions the array into two halves in such a way that the elements in the left sub array are less then and the elements in the right subarrays are are greater then the pivot element. And we apply the same algorithm on left subarray and right subarray separately (recursive).
Steps of Quicksort
1) Divide :Rearrange the elements and split the array into two sub arrays and an element in between .Each element in the left sub array is less than or equal to the middle element and each element in the right sub array is greater than the middle element.
2) Conquer : Apply step 1 recursively on two sub arrays.
3) Combine : Combine all the sorted elements in a group to form a list if sorted elements.
Example: We will sort an array
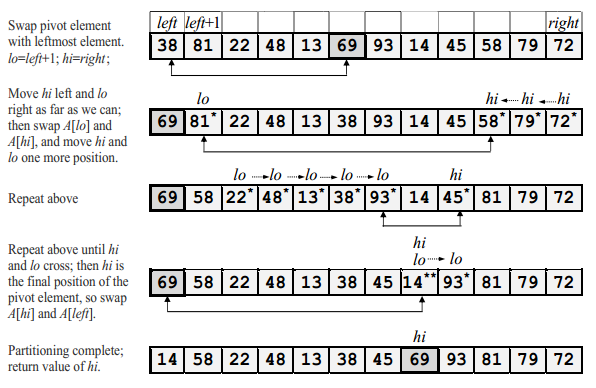
A = (38 81 22 48 13 69 93 14 45 58 79 72)
with quicksort, always choosing the pivot element to be the element in position (left + right)/2.
During the partitioning process,
i) Elements strictly to the left of position lo are less than or equivalent to the pivot element (69).
ii) Elements strictly to the right of position hi are greater than the pivot element. When lo and hi cross, we are done. The final value of hi is the position in which the partitioning element ends up.
Algorithm
partition( A, left, right) rarranges A[left..right] and finds and returns an integer q, such that
A[left], ..., A[q–1] <∼ pivot, A[q] = pivot, A[q+1], ..., A[right] > pivot,
Integer partition( T A[], Integer left, Integer right)
m = (left +right) / 2;
swap( A[left], A[m]);
pivot = A[left];
lo = left+1;
hi = right;
while(lo ≤ hi)
while(A[hi] > pivot )
hi = hi – 1;
while(lo ≤ hi and A[lo] <∼ pivot )
lo = lo + 1;
if (lo ≤ hi)
swap( A[lo], A[hi]);
lo = lo + 1;
hi = hi – 1;
swap(A[left], A[hi]);
return hi
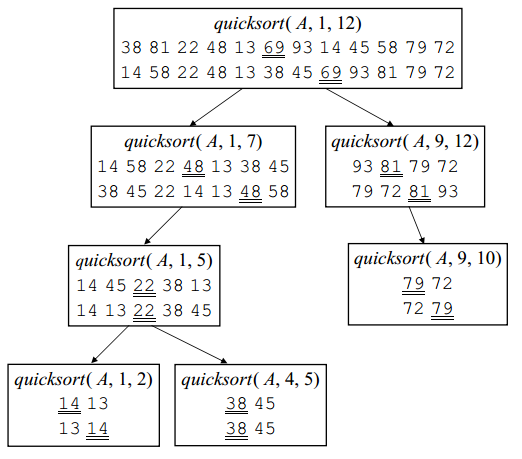
quicksort( A, left, right) sorts A[left..right] by using partition() to partition A[left..right], and then calling itself recursively twice to sort the two subarrays.
void quicksort( T A[], Integer left, Integer right)
if (left < right )
q = partition( A, left, right);
quicksort( A, left, q–1);
quicksort( A, q+1, right);
Complexity
Worst-case O(N2) This happens when the pivot is the smallest (or the largest) element. Then one of the partitions is empty, and we repeat recursively the procedure for N-1 elements.
Best-case O(NlogN) The best case is when the pivot is the median of the array, and then the left and the right part will have same size.
Average-case O(NlogN)
