top button
Flag Notify
    Connect to us
      Site Registration

Site Registration

Short notes on Quick Sort

0 votes
2,417 views

Quick Sort

Quick sort is a very popular sorting method. This sort name comes from the fact that quick sort can sort a list of data elements significantly faster than any of the common sorting algorithms. This sorting uses a strategy called divide and conquer. It is based on the principle that is faster and easier to sort two small arrays than one larger one. 

The sequence of steps required to perform a quick sort operation on a set of elements of  the array are as follows.

  1. A pivot item near the middle of the array is chosen. Let it be x.
  2. Now scan the array from left to right until some element e.g., ai>x is encountered.
  3. Now scan the array from right to left until some element e.g.,aj<x is encountered.
  4. Now exchange the items ai and aj.
  5. Again repeat steps 2 to 4 until the scan operation meets somewhere in the middle of the array.

Quick sort is also called partition exchange sort and it was invented by C.A.R. Hoare. The average execution time of quick sort is O(n(log2n)2) and this sort is good for large sorting jobs.

Pictorial Representation

 

 

Quick Sort Algorithm

1. If n < = 1, then return.

2. Pick any element V in a[]. This is called the pivot.

3. Rearrange elements of the array by moving all elements xi > V right of V and all elements x­i < = V left of V. If the place of the V after re-arrangement is j, all elements with value less than V, appear in a[0], a[1] . . . . a[j – 1] and all those with value greater than V appear in a[j + 1] . . . . a[n – 1].

4. Apply quick sort recursively to a[0] . . . . a[j – 1] and to a[j + 1] . . . . a[n – 1].

Program for Quick Sort 

#include <stdio.h>

void quick_sort(int[], int, int);
int partition(int[], int, int);

int main() 
{
    int a[50], n, i;

    printf("How many elements?");
    scanf("%d", & n);
    printf("\nEnter array elements:");

    for  (i = 0; i < n; i++)
    {
        scanf("%d", & a[i]);
    }

    quick_sort(a, 0, n - 1);

    printf("\nArray after sorting:");

    for (i = 0; i < n; i++)
    {  
        printf("%d ", a[i]);
    }


    return 0;
}

 

void quick_sort(int a[], int l, int u) 
{
    int j;

    if  (l < u) 
    {
        j = partition(a, l, u);
        quick_sort(a, l, j - 1);
        quick_sort(a, j + 1, u);
    }
}

 

int partition(int a[], int l, int u) 
{
    int v, i, j, temp;
    v = a[l];
    i = l;
    j = u + 1;

    do 
    {
        do
        {
            i++;
        }

        while (a[i] < v && i <= u);

        do
        {
            j--;
        }

        while (v < a[j]);

        if  (i < j)
        {
            temp = a[i];
            a[i] = a[j];
            a[j] = temp;
        }
    } 

    while (i < j);

    a[l] = a[j];
    a[j] = v;

    return (j);

}

The complexity of the quick sort algorithm is given in the following table.

Algorithm Worst case Average case Best case
Quick sort O(n)2 log2n log2n
posted May 2, 2017 by Sandeep Jain

  Promote This Article
Facebook Share Button Twitter Share Button LinkedIn Share Button


Related Articles

Short Notes On Queue

A Queue is a linear data structure. It is a list in which all insertions to the queue are performed at one end and all the deletions are performed at the other end. The element in the queue are processed in the same order in which they were received. Hence it is called a First In First Out(FIFO) list.

Applications of Queue

  1. Serving requests on a single shared resource, like a printer, CPU task scheduling etc.
  2. In real life, Call Center phone systems will use Queues, to hold people calling them in an order, until a service representative is free.
  3. Handling of interrupts in real-time systems.

Basic operation 

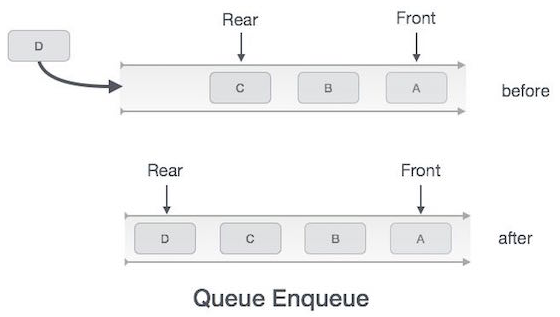
  • enqueue() − add (store) an item to the queue.

  • dequeue() − remove (access) an item from the queue.

Enqueue Operation

Queues maintain two data pointers, front and rear.

The steps should for enqueue (insert) data into a queue −

Step 1 − Check if the queue is full.

Step 2 − If the queue is full, produce overflow error and exit.

Step 3 − If the queue is not full, increment rear pointer to point the next empty space.

Step 4 − Add data element to the queue location, where the rear is pointing.

Step 5 − return success.

Dequeue Operation

Accessing data from the queue is a process of two tasks − access the data where front is pointing and remove the data after access.

Step 1 − Check if the queue is empty.

Step 2 − If the queue is empty, produce underflow error and exit.

Step 3 − If the queue is not empty, access the data where front is pointing.

Step 4 − Increment front pointer to point to the next available data element.

Step 5 − Return success.

 

Array Implementation Of Queue

#include <stdio.h>

#define MAX 50

int queue_array[MAX];

int rear = - 1;

int front = - 1;

main()

{

    int choice;

    while (1)

    {

        printf("1.Insert element to queue \n");

        printf("2.Delete element from queue \n");

        printf("3.Display all elements of queue \n");

        printf("4.Quit \n");

        printf("Enter your choice : ");

        scanf("%d", &choice);

        switch (choice)

        {

            case 1: insert();

            break;

            case 2: delete();

            break;

            case 3: display();

            break;

            case 4: exit(1);

            default: printf("Wrong choice \n");

        }   /*End of switch*/

    }   /*End of while*/

}   /*End of main()*/

insert()

{

    int add_item;

    if (rear == MAX - 1)

       {         

    printf("Queue Overflow \n");        

       }

    else

    {

        if (front == - 1)           

           {

        /*If queue is initially empty */

        front = 0;

        printf("Inset the element in queue : ");

        scanf("%d", &add_item);

        rear = rear + 1;

        queue_array[rear] = add_item;

           }

    }

} /*End of insert()*/

 

delete()

{

    if (front == - 1 || front > rear)

    {

        printf("Queue Underflow \n");

        return ;

    }

    else

    {

  printf("Element deleted from queue is : %d\n", queue_array[front]);

  front = front + 1;

    }

} /*End of delete() */

display()

{

    int i;

    if (front == - 1)        

       {

        printf("Queue is empty \n");

       }

    else

    {

        printf("Queue is : \n");

        for (i = front; i <= rear; i++)

            {

            printf("%d ", queue_array[i]);             

            printf("\n");

            }

    }

}

  Analysis of Queue

  • Enqueue : O(1)
  • Dequeue : O(1)
  • Size       : O(1)

Please go through video:

https://www.youtube.com/watch?v=okr-XE8yTO8

 

 READ MORE
Summary on bubble sort

Bubble Sort:-

Bubble sort is a simple sorting algorithm. This sorting algorithm is comparison-based algorithm in which each pair of adjacent elements is compared and the elements are swapped if they are not in order. Bubble sort algorithm starts by comparing the first two elements of an array and swapping if necessary, i.e., if you want to sort the elements of array in ascending order and if the first element is greater than second then, you need to swap the elements but, if the first element is smaller than second, you mustn't swap the element. Then, again second and third elements are compared and swapped if it is necessary and this process go on until last and second last element is compared and swapped.

Note: If there are n elements to be sorted then, the process mentioned above should be repeated n-1 times to get required result.

Algorithm:-

Step 1: Repeat Steps 2 and 3 for i=1 to 10

Step 2: Set j=1

Step 3: Repeat while j<=n

         (A) if  a[i] < a[j]

             Then interchange a[i] and a[j]

             [End of if]

         (B) Set j = j+1
        [End of Inner Loop]

    [End of Step 1 Outer Loop]

Step 4: Exit

Pictorial Representation
 

C program for bubble sort

   #include<stdio.h> //header files

   #include<conio.h>

void bubble_sort(int[], int);

      void main()      //starting of main function

 {

   int arr[30], num, i;    //array of size 30

  printf("\nEnter no of elements :");

   scanf("%d", &num);

   printf("\nEnter array elements :");

   for (i = 0; i < num; i++)

   scanf("%d", &arr[i]);

   bubble_sort(arr, num);     //calling the function

   getch(); //to hold the screen

 }

void bubble_sort(int iarr[], int num) 

{

   int i, j, k, temp;

   printf("\nUnsorted Data:");

   for (k = 0; k < num; k++) 

        {

      printf("%5d", iarr[k]);

        }

      for (i = 1; i < num; i++) 

            {

      for (j = 0; j < num - 1; j++) 

                 {

           if (iarr[j] > iarr[j + 1]) 

                       {

            temp = iarr[j];

            iarr[j] = iarr[j + 1];

            iarr[j + 1] = temp;

                       }

                 }

      printf("\nAfter pass %d : ", i);

      for (k = 0; k < num; k++) 

               {

         printf("%5d", iarr[k]);

               }

         }

}

Complexity:-

AlgorithmWorst caseAverage caseBest case
Bubble sort     O(n2)     O(n2)    O(n)

 

 READ MORE
Summary on insertion sort

Insertion Sort:

Insertion Sort is implemented by inserting a particular element at the appropriate position. The number of iterations used by this sorting technique depends on the number of items in the array. In general, if there are n items in the array, then (n-1) iterations are used. Here, we are going to implement this algorithm using C. In C, the array index starts from 0.

 

Algorithm:

1) Start.

2) Assume that there are n elements in the list of items to be sorted.

3) Set i=1,j=0.

4) Compare the element at the ith position and the element at the jth  position.

      a) If a[i] is greater than a[j] do the steps (i),(ii),(iii)

             i) temp=a[j]

            ii) a[j]=a[i]

            iii) Check if shifting is required. If so, do steps Ò

                     Ò k=i

                     Ò f (k is greater than j do step ►

                               ► a[k]=a[k-1]

                               ► k=k-1

                               ► go to Step (a)

                      Ò a[k+1]=temp

      b) j=j+1

          if(j<1) go to Step (a)

          Otherwise

          i=i+1

          j=0

          if(i<=n-1) go to Step (a)

5) Print the elements in the array a

6) Stop.

During the first iteration, the element at the 1st position is compared with the element at the 0th position. During the second iteration, the element at the 2nd position is compared with elements at the 0th and 1st positions. This process is repeated for all the elements in the array up to (n-1)st iteration. This method is widely used by card players.

 

Pictorial Representation

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Corresponding C program

#include<stdio.h>    //Header Files

#include<conio.h>

#include<math.h>

#include<stdlib.h>

void main()

{

        void isort(int a[],int);

        int s,a[50],t,n,i,j,k;

        clrscr();

        printf("Enter Total nos:");

        scanf("%d",&n);

        printf("\nEnter the Items 1 by 1:");

        for(i=0;i<n;i++)

             scanf("%d",&a[i]);

        isort(a,n);

        getch();

}

void isort(int x[],int n)

{

          int k,y,i;

          for(k=1;k<n;k++)

             {

                   y=x[k];

                   for(i=k-1;i>=0;i--)

                       {

                           if(y>=x[i]) 

                                break;

                           x[i+1]=x[i];

                       }

               x[i+1]=y;

             }

 

   printf("The Sorted Numbers are:\n");

   for(k=0;k<n;k++)

        printf("%d   ",x[k]);

}    

 

Complexity  The complexity of the insertion sort algorithm is shown in the following table. 

AlgorithmWorst caseAverage caseBest case
Insertion sort      O(n2)       O(n2)   O(n-1)
 READ MORE
...