How long is the lake, and what is the ratio of speeds between the purple and black boats?

Question

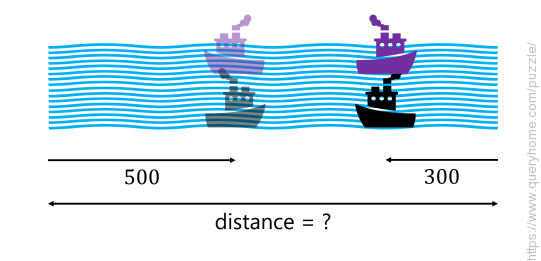
A black boat is on shore A and a purple boat is on the opposite shore B of a lake. Each boat starts at the same time for the opposite shore.

The boats meet and pass each other 500 units from shore A. Each boat gets to the opposite shore and immediately starts a return journey. The two boats then meet and pass 300 units from shore B.

How long is the lake, and what is the ratio of speeds between the purple and black boats?

Answer 1

The total length is 1200 units.
Relative speed is 5 units / time for black and 7 units / time for purple.
.
t1 = time to 1st crossing, t2 = time to 2nd crossing
y = total length
v1 = speed black, v2 = speed purple
t1 * v1 = 500
t1 * v2 = y - 500
t2 * v1 = y + 300
t2 * v2 = 2y - 300
v2 * (y + 300) = v1 * (2y - 300)
v2 * 500 = v1 * (y - 500)
v2 = v1 * y / 500 -v1
(v1 * y / 500 - v1) * (y + 300) = v1 * (2y - 300)
(y / 500 - 1) * (y + 300) = 2y - 300
1/500*y^2 = (2 + 2/5) * y
1/500 *y = 2.4
y = 1200
v1 / v2 = 5 / 7