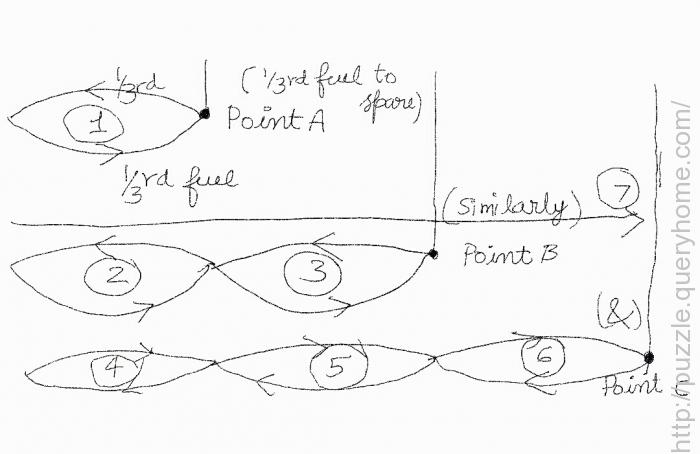
It will take seven planes to do this.
1st plane will be looping from Base to 1/6th point and back so at the 1/6th point it will have 1/3rd fuel to give each time. Let's call this point A.
Now similarly 2 (ie., 2nd and 3rd) planes can form such loop at the 1/6th the and 1/3rd points with the 3rd plane looping such that it meets with the 2nd plane refuel there and goes to 1/3rd point and is able to spare 1/3rd fuel. Let this be point B
Just like this the 4th, 5th and the 6th can form a triple loop that spans half the distance where the 6th will also be able to spare 1/3rd fuel at the end. Let this be point C.
Now the 7th plane will be able to refuel at the points A,B & C and have enough fuel for a round trip.
Please note here that the planes that form the loops can also refuel at points A and B to be able to spare fuel and once they are not needed all the planes starting from the farest will have enough fuel to get back to the airport.
