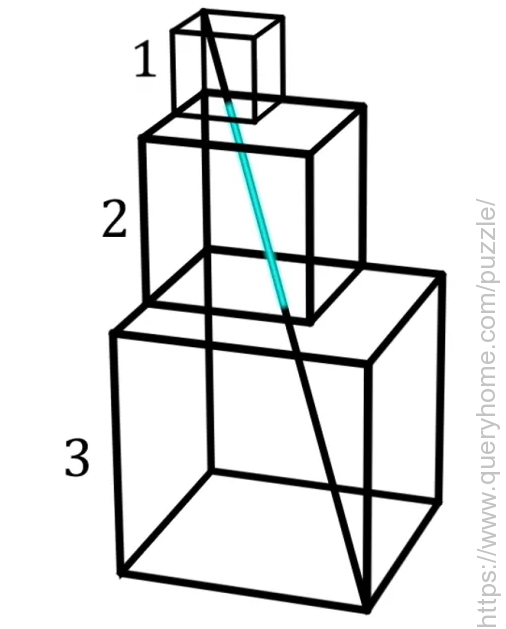
Cubes with edge lengths of 3, 2, and 1 are stacked in order with their left and back faces aligned, as shown below. A line is drawn between opposite corners of the bottom face of the 3 cube and the top face of the 1 cube.
What is the length of the line contained inside the middle cube?